Оптимальное обнаружение сигнала, о котором кое-что известно

В применении к АОНу в качестве измеренного уровня сигнала выражаемого числом выступает реализация сигнала на интервале времени выражаемая функцией.

Рассмотрим сигнал, генерируемый при передаче цифры 1 в стандарте АОНа, на интервале 10 мс

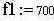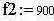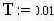		-временной интервал	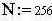-количество выборок



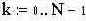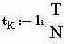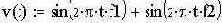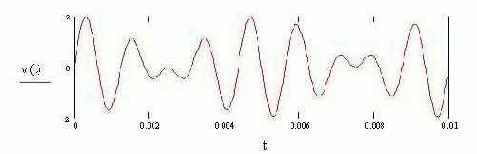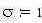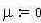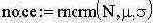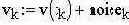	- наложим шум где m – мат. ожидание, s- стандартное отклонение
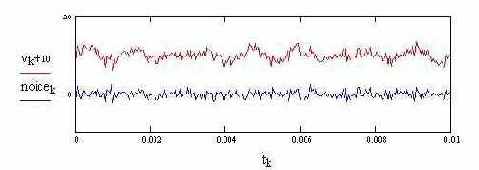- верхний график, реализация сигнала в смеси с шумом - нижний график, реализация шума

Вся крива, изображающая сигнал в совокупности, называется реализацией случайной функции. Свойства случайных функций изучаются в разделе случайные функции теории вероятностей. Наиболее полезный раздел - спектральная теория стационарных случайных функций. К сожалению, это довольно объемная теория и в двух словах ее здесь не перескажешь. Достаточно сказать, что сигнал рассматривается как стационарная случайная функция (поскольку случайны фаза и амплитуда), а шум как белый гаусовский шум с ограниченным спектром.

В случае с АОНом нам надо принять решение является ли наблюдаемая нами реализация шумом или смесью сигнала с шумом. Под сигналом мы здесь принимаем одну из тональных частот присутствующую в сигнале АОНа. Следовательно, нам надо принять 6-ть решений для каждой частоты: 700, 900, 1100, 1300, 1500, 1700 Гц.

Доказано, что плотность вероятности реализации гаусовского шума n1 (t) выражается формулой

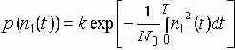Где N0 - спектральная интенсивность шума, k - постоянный множитель не зависящий от t .

Индекс 1 при n обозначает одномерное распределение.

Если проще сказать, то есть формула с помощью которой можно вычислить отношение правдоподобия основываясь на реализации сигнала на интервале времени и знании об интенсивности шума. Отношение правдоподобия L(u) выглядит следующим образом:

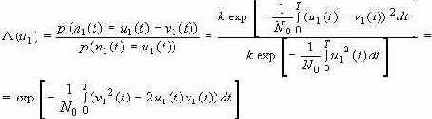Где u1 (t) - реализация принятого сигнала, v1 (t) - реализации ожидаемого сигнала, k - постоянный множитель, не зависящий от t , N0 - спектральная интенсивность шума.

Запишем формулу ожидаемого сигнала

Понятно, что у ожидаемого сигнала фаза представляет собой случайный параметр. Тогда отношение правдоподобия является функцией еще одной переменной ? - фазы ожидаемого сигнала. Для устранения неопределенности проводят статистическое усреднение отношения правдоподобия по этой переменной путем интегрирования. В результате чего приходят к формуле достаточно сложной:

Где I0 - модифицированная функция Бесселя первого рода нулевого порядка. V1 (t) - амплитуда ожидаемого сигнала.

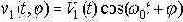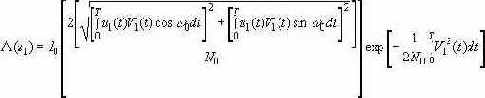Из формулы видно, что выражение под корнем можно вывести из всех остальных составляющих в формуле, таким образом, определив структуру оптимального обнаружителя

Интересно, что функция взаимно корреляционного устройства может быть выполнена фильтром, импульсная характеристика которого является зеркальным отражением ожидаемого сигнала. (т.к. операция свертки, осуществляемая фильтром, и корреляции описываются одинаковыми математическими формулами). Поэтому в литературе часто можно встретить описание оптимальных фильтров (не путать с оптимальными фильтрами не в контексте оптимального обнаружения).

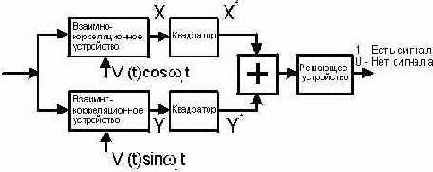Приведенная формула позволяет определить структуру оптимального фильтра, но в реальных условиях недостаточно адекватна. С одной стороны реальный шум весьма далек от белого, с другой, здесь не учтено влияние помех и соседних частот посылки АОН. Поэтому остается необходимость в имитационном моделировании, которое дало бы ответы на вопрос о выборе оптимальной границы в условия влияния разных факторов, не учитываемых формулой.

Но для начала проверим, какое влияние окажет на спектр сигнала предельное ограничение его амплитуды, которое производится компаратором.

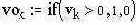	сформируем предельно ограниченный сигнал
	- спектр входного сигнала
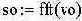	- спектр предельно ограниченного сигнала

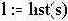Как видно, с небольшим масштабированием, спектр преобразованного сигнала мало изменился по сравнению со спектром исходного. Эта особенность с успехом применяется в АОНах, где вместо АЦП применяют компаратор. С другой стороны предельное ограничение позволяет избавиться от неопределенности амплитуды сигнала и шума, что делает более надежной работу оптимального обнаружителя

Содержание раздела